This post explains a mechanism for the mouse to stick translation, that allows to reach a better precision and that is required to perform a 1:1 translation.
If you don’t want to read some math, then skip this post 🙂
All values are considered positive so as to simplify the explanation.
Each 10 ms, the sixaxis emulator processes all pending events.
All mouse motion events are merged and as a result, a single mouse event is processed.
This mouse event contains cumulated x and y deltas: (dx1, dy1).
This motion vector is then translated into a stick position according to the following formula:
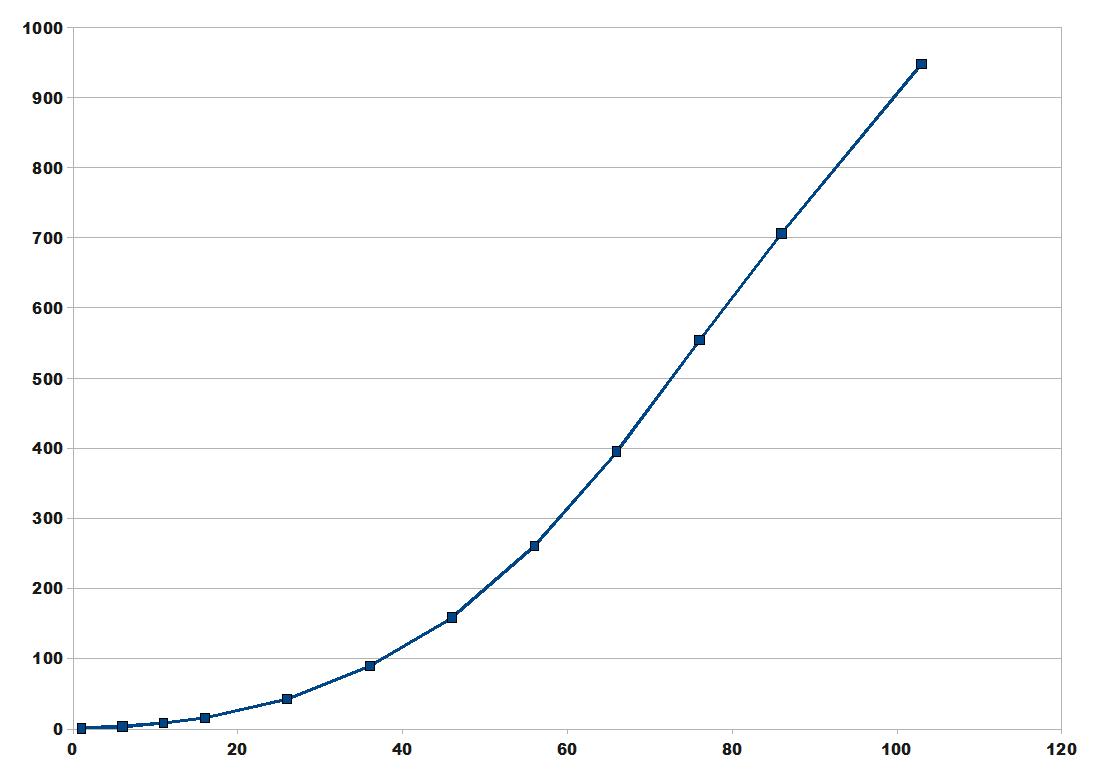
(1) pos1 = dz1 + mul * pow(mv1, exp)
pos1 = desired stick position (real)
dz1 = deadzone (real, function of dx1, dy1 and the deadzone shape)
mv1 = mouse value (integer), dx1 or dy1
mul = multiplier (real, constant)
exp = exponent (real, constant)
The result pos1 is a real. But the final stick position has to be an integer.
What emuclient was doing previously is rounding pos1 to the nearest integer.
This obviously results into a lower or higher speed than the desired one.
A much more precise solution to tackle this real to integer conversion is to truncate pos1, and compute a mouse vector remainder to be added next iteration.
The mouse event that corresponds to the applied stick position is: (dx2, dy2).
dx2 and dy2 are reals.
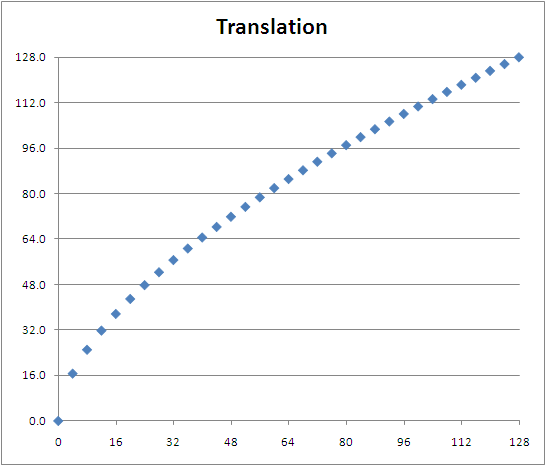
(2) pos2 = dz1 + mul * pow(mv2, exp)
pos2 = applied stick position (truncate(pos1), integer)
dz1 = deadzone (same value, the angle is considered to be the same)
mv2 = mouse value (real), dx2 or dy2
mul = multiplier (real, constant)
exp = exponent (real, constant)
Note: norm(mv1) >= norm(mv2)
(3) vrem = mv1 - mv2
vrem = mouse vector remainder
mv1 is known.
mv2 is computed from (2):
(4) mv2 = pow[(pos2 - dz1)/mul, 1/exp]
mv2 can be replaced in (3):
(5) vrem = mv1 - pow[(pos2 - dz1)/mul, 1/exp]
Conclusion:
- (5) gives the mouse vector remainder that has to be added the next iteration
- this emulates a subposition precision
Notes:
- this is useful with 8-bit precision for stick axes as the speed difference between two neighbor stick positions is high
- this is useless with 16-bit precision for stick axes